Μηδείς αγεωμέτρητος εισίτω

Εγκώμιο για τα μαθηματικά
του Alain Badiou (με τον Gilles Haéri) 
Μετάφραση: Φώτης Σιατίτσας
εκδ. Πατάκη 2017, 132 σελίδες

Ο Αλέν Μπαντιού (Alain Badiou) είναι πια αρκετά γνωστός στο ελληνικό αναγνωστικό κοινό. Περισσότερο, βέβαια, για τις παρεμβάσεις του σχετικά με την Κομμουνιστική υπόθεση, παρά για το κατεξοχήν φιλοσοφικό του έργο. Κι αυτό όχι επειδή τα γραπτά του είναι δύσκολα προσβάσιμα στο ελληνικό κοινό. Το αντίθετο, πολλά και πολύ σημαντικά του κείμενα κυκλοφορούν ήδη στη γλώσσα μας, σε πολύ καλές και επιμελημένες μεταφράσεις. Στην πραγματικότητα, οι απαιτήσεις που θέτει η ανάγνωση του έργου του, σε αντίθεση με των «νέων» φιλοσόφων, είναι που το κάνει «δύσκολο». Επιπλέον, η ίδια η φιλοσοφική του στάση, με την επικέντρωση στα κλασικά αντικείμενα, χωρίς καμιά έγνοια –το αντίθετο, μάλιστα– να επιδείξει την πρέπουσα (!) απέχθεια προς τη «μεταφυσική», τον βγάζει εκτός τροχιάς της σύγχρονης φιλοσοφίας, αναλυτικής ή μεταμοντέρνας.

Το Εγκώμιο για τα μαθηματικά , μια συζήτηση ανάμεσα στον Μπαντιού και τον Ζιλ Ερί (Gilles Haéri), δίνει μια μοναδική, νομίζω, δυνατότητα να εισαχθούμε στο έργο του με ένα γοητευτικό και διανοητικά ερεθιστικό τρόπο. Μ’ όλο που το θέμα είναι τα μαθηματικά, είναι πολλές οι αφορμές και οι ομαλές παρεκβάσεις που επιτρέπουν την πρόσβαση σε θεμελιώδεις ιδέες, καταστατικές της φιλοσοφίας του Μπαντιού. Η Αλήθεια και το Συμβάν παρεισφρέουν σε πολλά σημεία της συζήτησης, παρωθώντας σε μια αρχική κατανόηση ή σε μια πρόσληψη της εννοιολογικής σκευής του φιλοσόφου μέσα από συγκεκριμένα παραδείγματα.

Συζητώντας θέματα, όπως τη θεμελιακότητα των μαθηματικών για κάθε συγκροτημένη μορφή σκέψης, τη σχέση της φιλοσοφίας με τα μαθηματικά ή τη σχέση τους με την ευτυχία, ο Μπαντιού βρίσκει την ευκαιρία να τοποθετηθεί σε θεμελιώδη, από τις προσωκρατικές απαρχές ήδη, προβλήματα. Ενδιατρίβοντας σε ερωτήματα σχετικά με το «για ποιο πράγμα μιλάνε τα μαθηματικά» ή για το «πώς είναι δυνατή μια μεταφυσική στηριγμένη στα μαθηματικά» μιλά ευρύτερα για τα «πράγματα» και για τη μεταφυσική.

Γιατί, όμως, τα μαθηματικά; Καταρχήν γιατί έτσι το θέλησε η τύχη: ο πατέρας του ήταν καθηγητής των μαθηματικών. Κατόπιν, όμως, και αφού η τύχη είχε κάνει τη δουλειά της, ανέλαβε η αισθητική. Όπως πολύ γλαφυρά εξηγεί, είναι αδύνατο, στο μέτρο που κάποιος το κατανοήσει –και δεν είναι πολύ δύσκολο αυτό–, να μην συγκλονιστεί με το τόσο ανέλπιστο, τόσο κομψό δώρο προς την όραση, όσο και την νόηση, που αποτελεί η ευθεία του Όιλερ. Για θυμηθείτε: Τα τρία ύψη ενός τριγώνου συντρέχουν σε ένα σημείο Η –ήδη αυτό είναι υπέροχο. Οι τρεις μεσοκάθετοι συντρέχουν, επίσης, σε ένα σημείο Ο –όλο και καλύτερα. Τέλος, οι τρεις διάμεσοι συντρέχουν και αυτές σε ένα τρίτο σημείο Λ –καταπληκτικό. Και το θαύμα συνεχίζεται: τα σημεία Η, Ο και Λ βρίσκονται στην ίδια ευθεία!

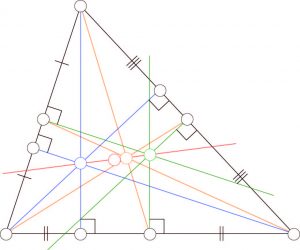
Είναι παράξενο, μετά από αυτό, που ο Αριστοτέλης θεωρούσε ότι τα μαθηματικά αφορούν, περισσότερο και από την αλήθεια, το κάλλος; Και επομένως ότι σχετίζονται με την ομορφιά τόσο όσο και  με την οντολογία;

Εξάλλου οντολογία και μαθηματικά είναι άμεσα συνδεδεμένα. Πρώτα πρώτα, γιατί οι δομές εν γένει είναι υπόθεση των μαθηματικών. Ο Μπαντιού θα θυμίσει, στη διάρκεια της συζήτησης, πόσο στα χρόνια του δομισμού  όλοι αντιλαμβάνονταν πως χωρίς μαθηματικά δουλειά δεν μπορούσε να γίνει επ’ ουδενί. Ο Λεβί Στρως, προκειμένου να μελετήσει τις «στοιχειώδεις δομές της συγγένειας», ήταν υποχρεωμένος να προσφύγει στην αλγεβρική θεωρία ομάδων.

Δεν πρόκειται όμως μόνο για τις δομές στον πληθυντικό. Είναι και η δομή στον ενικό, η δομή του είναι ως είναι. Η σκέψη πάνω στη δομή, η σκέψη πάνω στο είναι προϋποθέτει τα μαθηματικά. Με τα λόγια του Μπαντιού, «τα μαθηματικά ενδιαφέρονται, η επικεντρώνουν την προσοχή τους στην πιο τυπική, την πιο αφηρημένη, την πιο καθολικά σχεδόν κενή διάσταση του είναι ως τέτοιου. Είναι εύκολο  να υποστηρίξουμε […] πως ό,τι υπάρχει αποτελεί μια πολλαπλότητα. Έτσι, θα υποστηρίξουμε ότι τα μαθηματικά, ως η γενική θεωρία των διαφόρων μορφών στις οποίες οι πολλαπλότητες αποκτούν μια ορισμένη συνέπεια, συνιστούν μια θεωρία αυτού που είναι, όχι στο βαθμό που είναι τούτο ή εκείνο, αλλά απλά στον βαθμό που είναι» (σελ. 46).

Η ισχυρή –και πολύ πειστική– εκδοχή αυτής της ιδέας είναι πως η φιλοσοφία είναι αδύνατη χωρίς τα μαθηματικά.  Έτσι ο Μπαντιού υπαινικτικά, αλλά καθόλου διακριτικά, θα χλευάσει τη «νέα» φιλοσοφία, ακριβώς στο μέτρο, που είναι ολοκληρωτικά «αγεωμέτρητη», και μάλιστα το περηφανεύεται συχνά. Θα αναφερθεί στη μακρά σειρά των φιλοσόφων, από τον Παρμενίδη, τον Πλάτωνα και τον Αριστοτέλη μέχρι τον Καρτέσιο, τον Λάιμπνιτς, τον Σπινόζα, τον Καντ, τον Χέγκελ ή τον Ράσελ και τον Ουάιτχεντ, μεταξύ πολλών πολλών άλλων, προκειμένου να δείξει, σχεδόν με το δάχτυλο, πόσο δικαιώνεται η κρίση ότι τα μαθηματικά είναι αναγκαία για τη φιλοσοφία. Πολύ τον διασκεδάζει η ιδέα πως πολυάριθμοι «σπινοζιστές», πεπεισμένοι για την μοναδικότητα της Υπόστασης και την εμμένεια της κίνησης του κόσμου, στέκονται με αμηχανία μπροστά σε μια πρωτοβάθμια εξίσωση.

Αλήθεια, πόσο είναι δυνατό να κατανοήσουμε την διαχρονική οντολογική συζήτηση, χωρίς να προσφύγουμε καταστατικά στις μαθηματικές –και μόνο μαθηματικές– έννοιες του απείρου ή της σύγχρονης λογικής, τυπικής, ιντουσιονιστικής ή παρασυνεπούς; Απλώς δεν γίνεται. Γι’ αυτό, ίσως, οι «νέοι» φιλόσοφοι εγκατέλειψαν την «παραδοσιακή» φιλοσοφική πρακτική και βρήκαν νόημα –πράγμα αδιανόητο για τον Χέγκελ, τον Κοντ, τον Σερλ ή τον Μπασελάρ– στην εξωφρενική ιδέα μιας εξειδικευμένης φιλοσοφίας.  «Η ιδέα ότι η φιλοσοφία μπορεί να είναι η φιλοσοφία τούτου ή εκείνου, ότι έχει «ειδικά» αντικείμενα, ανήκει στη σφαίρα αυτού που ο Λακάν αποκαλεί ‘λόγο του Πανεπιστημίου’, με τη χειρότερη έννοια του όρου. Η φιλοσοφία είναι ακριβώς η φιλοσοφία, δηλαδή αυτό που υποστηρίζει μια μοναδική και ολική σχέση με τους όρους (conditions) της και που ανάγω σε τέσσερα ‘είδη’, τα οποία είναι για μένα ισάριθμες μορφές εκείνου που αποκαλώ αλήθειες: οι επιστήμες: γνωσιακές αλήθειες, οι τέχνες: κατ’ αίσθηση αλήθειες, οι πολιτικές: συλλογικές αλήθειες, και οι έρωτες: υπαρξιακές αλήθειες» (σελ. 52-53). Που σημαίνει ότι τα μαθηματικά δεν προσφέρουν όλη την αλήθεια, αλλά και δεν είναι δυνατή η προσέγγιση της αλήθειας χωρίς τα μαθηματικά. Γιατί τα μαθηματικά, δηλαδή «η σχέση της σκέψης με το είναι ως είναι, δεν αντιπροσωπεύει βέβαια την ολότητα της σχέσης των υποκειμένων προς τον κόσμο, απολύτως όχι. Τα μαθηματικά δεν συνιστούν καθόλου την επιστήμη της διαφοράς ανάμεσα σε ένα φθινοπωρινό φύλλωμα και έναν καλοκαιρινό ουρανό. Λένε απλώς ότι, σε κάθε περίπτωση, όλα αυτά αποτελούν πολλαπλότητες, μορφές που έχουν κάτι κοινό, το γεγονός ότι, πολύ απλά, είναι» (σελ. 46).

Το Εγκώμιο για τα μαθηματικά είναι ένα έμπρακτο εγκώμιο στη σκέψη.